Introduction of Capacitor Energy And Time Constant Calculator
Calculate the energy (E) and time constant (RC) in a capacitor for a given voltage across it using an online capacitor energy (E) and RC time constant calculator. The capacitor energy and time constant calculator can be used to calculate two different values: the time constant (T) can be calculated using the values of capacitance (C) and load resistance (R), and the energy stored in a capacitor (E) can be calculated using all three inputs: voltage (V), capacitance, and load resistance.
What is Time Constant of capacitor ?
The time constant takes for a capacitor to charge up to full capacity is related to the circuit's capacitance and resistance. The circuit's resistance adds a time component to the charging and discharging of a capacitor.
A particular length of time is necessary for a full charge or discharge when a capacitior charges or discharges through a resistance. The voltage across the capacitor is not going to alter in a flash. The time constant of the circuit determines the pace of charging or discharging.
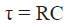
The time in the formula is the time it takes to charge to 63 percent of the source's voltage. The charge must be brought to around 99 percent of the source voltage in about 5 minutes. This connection of a time constant typical of charging is seen in the below picture.

Capacitance is a measurement of a capacitor's capacity to hold charge. The letter C is used to represent capacitance.
There can't be a continuous flow of direct current via a capacitor, as the time constant graphic shows. A good capacitor will stop direct current while allowing pulsating DC or alternating current to pass through.
How to calculate the time constant of a capacitor?
When a signal or voltage, either continuous (DC) or alternating (AC), is applied to any electrical or electronic circuit or system, there is some type of "time-delay" between the input and output terminals.
This delay is commonly referred to as the circuit's time delay or Temporal Constant, and it indicates the circuit's time reaction when a step voltage or signal is applied. The time constant of any electronic circuit or system is mostly determined by the reactive components linked to it, which might be capacitive or inductive. The time constant is measured in Tau-τ.
When a discharged capacitor is exposed to a rising DC voltage, the capacitor draws a "charging current" and "charges up." The capacitor begins to discharge in the opposite way when the voltage is dropped. Because capacitors can store electrical energy, they function similarly to miniature batteries in that they store and release energy on their plates as needed.
When a resistor is linked in series with a capacitor to form an RC circuit, the capacitor will progressively charge up through the resistor until the voltage across it equals the supply voltage. The time necessary to fully charge the capacitor is about 5 time constants, or 5T. As a result, a series RC circuit's transient response is equivalent to 5 time constants.
This transient reaction time, T, is expressed in seconds as = R x C, where R is the resistor value in ohms and C is the capacitor value in Farads. This is then used to build an RC charging circuit, with 5T standing for "5 x RC."
How to find the time constant?
As a result, the percentage of voltage and current values for the capacitor in an RC discharging circuit and RC charging circuit for a particular time constant may be found in the table below.
RC Discharging Table
Time Constant | RC Value | Percentage of Maximum | |
Voltage | Current | ||
0.5 time constant | 0.5T = 0.5RC | 39.30% | 60.70% |
0.7 time constant | 0.7T = 0.7RC | 50.30% | 49.70% |
1.0 time constant | 1T = 1RC | 63.20% | 36.80% |
2.0 time constants | 2T = 2RC | 86.50% | 13.50% |
3.0 time constants | 3T = 3RC | 95.00% | 5.00% |
4.0 time constants | 4T = 4RC | 98.20% | 1.80% |
5.0 time constants | 5T = 5RC | 99.30% | 0.70% |
RC Charging Table
Time | RC Value | Percentage of Maximum | |
Voltage | Current | ||
0.5 time constant | 0.5T = 0.5RC | 60.70% | 39.30% |
0.7 time constant | 0.7T = 0.7RC | 49.70% | 50.30% |
1.0 time constant | 1T = 1RC | 36.80% | 63.20% |
2.0 time constants | 2T = 2RC | 13.50% | 86.50% |
3.0 time constants | 3T = 3RC | 5.00% | 95.00% |
4.0 time constants | 4T = 4RC | 1.80% | 98.20% |
5.0 time constants | 5T = 5RC | 0.70% | 99.30% |
What is Capacitor Energy?
A capacitor is a typical electrical component in circuits. Its purpose is to store electrical energy. Charges of equal but opposite value are present on neighboring plates in typical parallel plate capacitors (for a spherical capacitor there are concentric spheres instead of plates). These charges form an electric field between them, which is made up of a portion of the energy in the circuit. This is an example of potential energy because we're talking about stored charges.
How to Calculate the energy stored in a capacitor?
Electrical potential energy is stored in a capacitor and is thus connected to the charge Q and voltage V on the capacitor. When using the equation for electrical potential energy qV to a capacitor, we must be cautious. Remember that a charge q passing through a voltage V has a potential energy of PE. The capacitor, on the other hand, begins with no voltage and progressively increases to its maximum value as it is charged. Because a capacitor has zero voltage when it is uncharged, the initial charge placed on it causes a voltage change of V = 0. Because the capacitor now has its full voltage V, the last charge placed on it experiences V = V.
During the charging process, the capacitor's average voltage is V/2, and so the average voltage experienced by the full charge q is V/2. Thus the energy stored in a capacitor, Ecap, is Ecap=QV/2, where Q is the charge on a capacitor with a voltage V applied. (Note that the energy is not QV, but QV/2.) Charge and voltage are related to the capacitance C of a capacitor by Q = CV, and so the expression for Ecap can be algebraically manipulated into three equivalent expressions:
Ecap=QV/2=CVV/2=QQ/2C
where Q is the charge and V the voltage on a capacitor C. The energy is in joules for a charge in coulombs, voltage in volts, and capacitance in farads.
How To Find the energy stored in a capacitor in series?
The Youtube Video titled with “How To Calculate The Energy Stored In a Capacitor”, This physics video lesson shows how to use three alternative formulae to compute the energy stored in a capacitor. It also describes how to determine the capacitance and voltage of a capacitor, as well as the power provided by a capacitor. Many practice problems on estimating the potential energy stored in capacitors may be found in this tutorial.
How To Calculate Energy Using Power and Time?
The quantity of electrical energy required by a given item may be easily determined, as can the cost of electrical energy utilized for that appliance.
Calculations of electrical energy
The quantity of electrical energy transmitted to an appliance is determined by its power and the time it has been turned on. Kilowatt-hours, or kWh, are the units of measurement for the quantity of mains electrical energy transported. 1 kWh equals one unit.
Electric Energy Formula
E = P × t
E is the energy transferred in kilowatt-hours, kWh
P is the power in kilowatts, kW
T is the time in hours, h.
It's worth noting that power is measured in kilowatts rather than the more common watts. You must divide by 1,000 to convert from W to kW.
For example, 1,000 W = 1,000 ÷ 1,000 = 1 kW.
It's also worth noting that here, instead of seconds, time is measured in hours. To convert seconds to hours, multiply the number by 3,600.
For example, 7,200 s = 7,200 ÷ 3,600 = 2 h.





















